St. Louis Rams $100K Giveaway

It was announced today that the St. Louis Rams are offering $100,000 to anybody who correctly predicts their 2014 schedule. The 16 opponents are known, so you must guess which opponent the Rams play each week, along with their bye week.  To make things more difficult, you must also predict if the game is played on Sun (which most are), Monday (typically 1 game each week), or Thursday (typically 1 game each week).

I did a quick back-of-the-envelope calculation to determine the approximate odds of winning such a contest and came up with 1 in 45,193,226,156,719,200 which is about "45 followed by 15 zeros".  Here's how I got this number:

First, let's choose the bye week.  Last year no teams had a bye in weeks 1-3 or 13-17. This leaves 9 choices for the bye week.

Next, we can place the 16 opponents among the remaining 16 weeks. This can be done 16! ways (reminder: 16! = 16 * 15 * 14 * ... * 2 * 1).  That's a lot of choices. However, the Rams play the 3 teams in their division twice each, and we can assume that they will not play the same team in consecutive weeks. Accounting for the bye week, this removes about 15 * 14 * 3 = 630 possibilities (although there is some double counting that I'm ignoring).

Finally, we need to select the day of the game.  On average, each team plays one Sunday night game and one Thursday night game. For simplicity, we will assume that the Rams will play exactly 1 Thurs. night and one Mon. night game.  Ignoring the bye week, this leaves 16 * 15 = 240 possibilities. (In reality, games that are thought to be "better" are on Monday night and games that are thought to be less interesting are played on Thursday. Therefore, the odds are probably slightly different).

To get the final number of possibilities, we need to multiply the different possibilities together: 9 * (16! - 630) * 240 = 45,193,226,156,719,200.  Although this is slim chances, I still took 5 minutes to fill out the schedule. So here's to hoping I'm $100,000 richer when I write my next post!

P.S. - I'm sure I made some silly mistake, so please comment if you notice one and I'll get it fixed.

Winter Olympics Medal Predictions Gone Wrong

I recently came across an article about an analytics company, MicroStrategy, that used their dashboard to predict the number of medals that each country will win at the 2014 Winter Olympics. They predicted that Canada will win the most medals (35), followed by Germany (31), with the US in 7th place (16 medals). They explain the results in their blog post. I think the company was just trying to do a simple, light-hearted analysis to show off the types of analyses that their product can do. Unfortunately for the company, there are several flaws in their model/analysis.  Two minor flaws have to do with the data itself:

• In their post, they state "Keep in mind that the algorithm is based on historical data, and doesn’t necessarily reflect more current information such as emerging stars, recent funding boosts, and an unexpectedly large addition of new events to the program."
• On a related note, they fail to explain how they handled the dissolution of old countries to form new countries. For example, are the medals from past Olympics won by the USSR now contributed to Russia? What about newer countries, such as Ukraine, that used to be a part of USSR?

The biggest problem is over-fitting of the model. Over-fitting occurs when you design a complex model using many variables that is more likely to describe random noise than the true signal. Because the model is describing the noise and not true signal of the historical data, it often results in inaccurate predictions (in this case, inaccurate medal predictions). If you are interested in performing predictions based on a model, one simple way to determine if a model is over-fit is by leaving out a subset of the data, fitting a model, then using that model to predict the data that you left out. Since you know the "truth" of these predicted data, you can assess the prediction accuracy. For example, MicroStrategy could have used all data prior to 2010, fit the model using that data, then predicted medal counts for 2010. We would be able to determine the accuracy by comparing to the true 2010 medal counts. 

The 2014 Winter Olympics are only half way over, but let's compare their predictions to current medal counts for selected countries:

	Predicted Medal Count	Actual Medal Count (as of 2/16)
Canada	35	14
Germany	31	12
Russia	18	16
USA	16	16
Netherlands	7	17

While it is possible that Canada and Germany can still reach their predicted medal counts, it looks like Russia, USA, and the Netherlands will all greatly surpass their predicted medal count.

Again, I realize that the company was doing this for fun and to generate some press. I just hope that customers don't look at this analysis, see how bad these predictions are, and ultimately decide to not buy the product. This goes to show how a little statistical knowledge can go a long way!

Battle of the Sexes: Free Throw Edition

As a UNC basketball fan, this season has definitely been a roller coaster ride.  UNC is 3-0 against top 25 teams, beating #1 Michigan State on the road, #3 Louisville on a neutral court, and #11 Kentucky at home.  UNC has also had some bad loses: UAB, Belmont, and Texas.  Two of the losses were by 3 points, and UNC missed over 20 free throws in both of those games.  Last weekend, I attended the Toledo-Dayton women's basketball game, and there were hardly any missed free throws.  So this got me thinking: are women any better than men at free throw shooting?

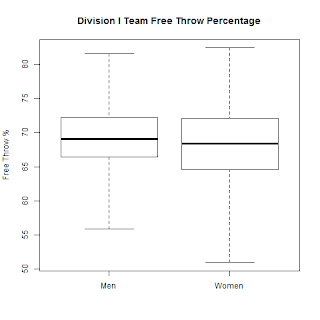
When looking at all Division I free throw percentages for both men and women (as of December 27), men are slightly better at making free throws, as shown below. The median free throw percentages (thick black lines) are 69.1% for men and 68.4% for women.  The variability is also much smaller for the men than women.  Note that the UNC men make 61.3% of their free throws, ranking them 333 out of all 345 teams.

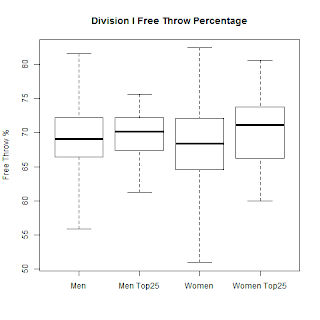
Next, I wanted to look the the free throw percentages of the top 25 ranked teams, which is shown below.  For easier comparison, I have also included the distribution for all Division I teams.

For both men and women, teams ranked in the top 25 are on average better at making free throws than compared to all teams.  When restricted to top 25 teams, women have a better free throw percentage than men.

So who is better at making free throws: men or women?  Men are slightly better on average than women, but when restricted to the best 25 teams, women are on average better.  Regardless, I'm hoping that UNC can increase their free throw percentage in the second half of this season.